컴퓨터 산술
- 정수(integer) 연산
- 덧셈, 뺄셈
- 곱셈, 나눗셈
- 오버플로 처리
- 부동소수점 실수(Floating-point real number)
- 표현 및 연산자
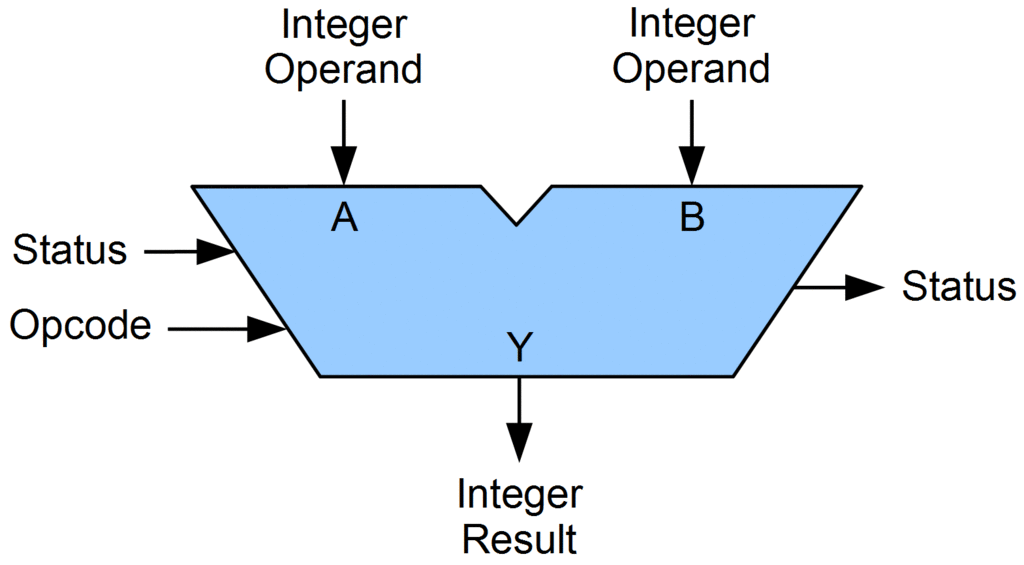
산술 논리 장치(ALU)
- 정수 이진수의 산술/비트를 연산하는 조합 디지털 전자 회로
- CPU, FPU, GPU를 포함한 다양한 컴퓨팅 회로의 기본 구성 요소
- 하나의 CPU, FPU, GPU에는 여러 ALU가 포함될 수 있다.
정수 덧셈
- 예) 7 + 6
- 결과가 범위를 벗어나면 오버플로가 발생한다.
- '+', '-' 피연산자 더하기
- 오버플로 없음
- 두 개의 '+' 피연산자 더하기
- 결과 부호(sign bit)가 1인 경우 : 오버플로
- 두 개의 '-' 피연산자 더하기
- 결과 부호(sign bit)가 0인 경우 : 오버플로
정수 뺄셈
- 두 번째 피연산자 부정
- 예) 7 - 6 = 7 + (-6)
+7 : 0000 0000 ... 0000 0111
-6 : 1111 1111 ... 1111 1010
+1 : 0000 0000 ... 0000 0001
- 결과가 범위를 벗어나면 오버플로가 발생
- 2개의 '+' 또는 2개의 '-' 피연산자 빼기
- 오버플로 없음
- '-' 피연산자에서 '+' 빼기
- 결과 부호(sign bit)가 0인 경우 오버플로
- '+' 피연산자에서 '-' 빼기
- 결과 부호(sign bit)가 1인 경우 오버플로
오버플로 다루기
- 일부 언어(예: C)는 오버플로를 무시한다.
- MIPS에서 addu, addui, subu 명령어를 사용한다.
- 다른 언어(예: Ada, Fortran)에서는 예외 발생이 필요하다.
- MIPS에서 add, addi, sub 명령어를 사용
- 오버플로 시 예외 처리기를 호출한다.
- 예외 프로그램 카운터(EPC) 레지스터에 PC를 저장한다.
- 미리 정의된 핸들러 주소로 점프한다.
- mfc0(move from 코프로세서 레지스터) 명령은 EPC 값을 검색하여 수정 조치 후 반환할 수 있다.
멀티미디어를 위한 산술
- 그래픽 및 미디어 처리는 8비트 및 16비트 데이터 벡터에서 작동한다.
- 분할된 캐리 체인이 있는 64비트 가산기를 사용한다.
- 8x8비트, 4x16비트, 2x32비트 벡터에서 작동
- 하나의 64비트는 비싸기 때문이다.
- SIMD(단일 명령, 다중 데이터)
- 분할된 캐리 체인이 있는 64비트 가산기를 사용한다.
- 포화 연산(Saturating operations)
- 오버플로 시 결과는 표현할 수 있는 가장 큰 값이다.
- 참조) 2의 보수 모듈로 연산
- 예) FF FF FF(RGB) + FF FF FF(RGB) = FF FF FF(RGB)
- 흰색 + 흰색 = 흰색(표현할 수 있는 가장 큰값)
- 예: 오디오 클리핑, 비디오 채도
- 오버플로 시 결과는 표현할 수 있는 가장 큰 값이다.
- 크기가 매우 크다.
- 예) 비디오 색 계산
곱셈
- 긴 곱셈 접근법으로 시작
1000 x 1001 = 1001000
1000 # multiplicand
x 1001 # multiplier
────
1000
0000
0000
1000
────
1001000 # product
- multiplicand : 1000
- multiplier : 1001
- product : 1001000
- 곱의 길이는 피연산자 길이의 합
- 32비트 x 32비트 → 64비트
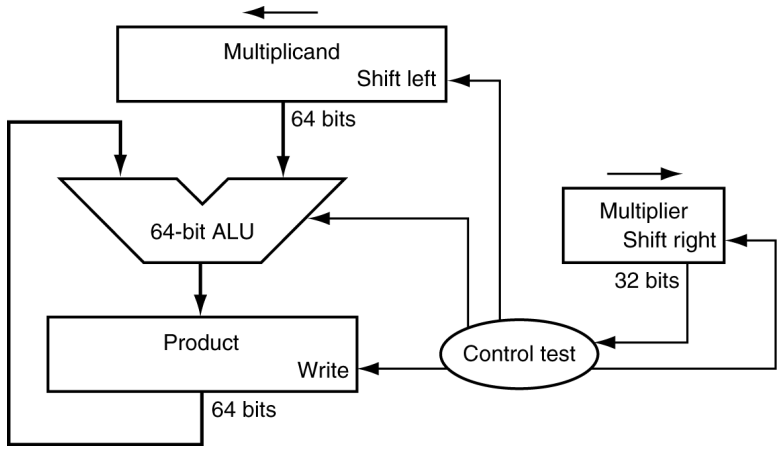
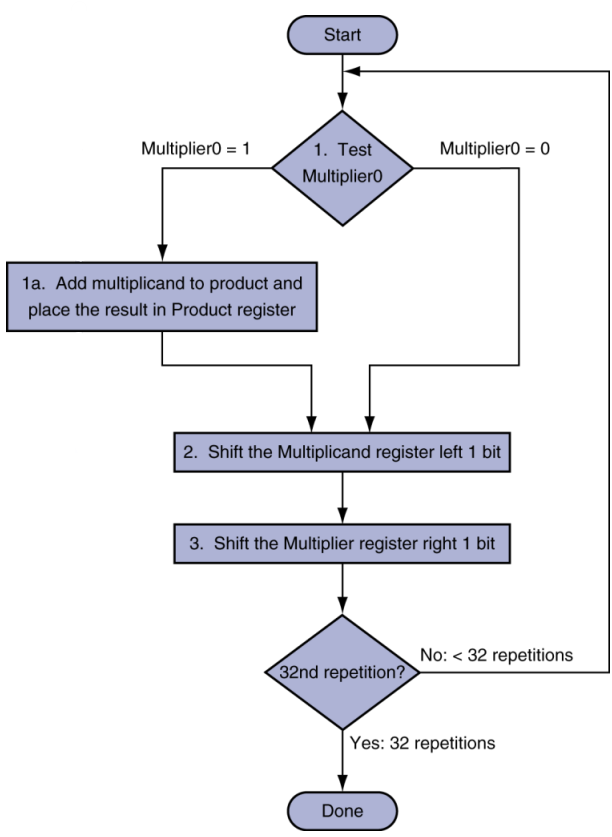
- 플로우차트
최적화 multiplier
- 병렬 단계 수행: add/shift
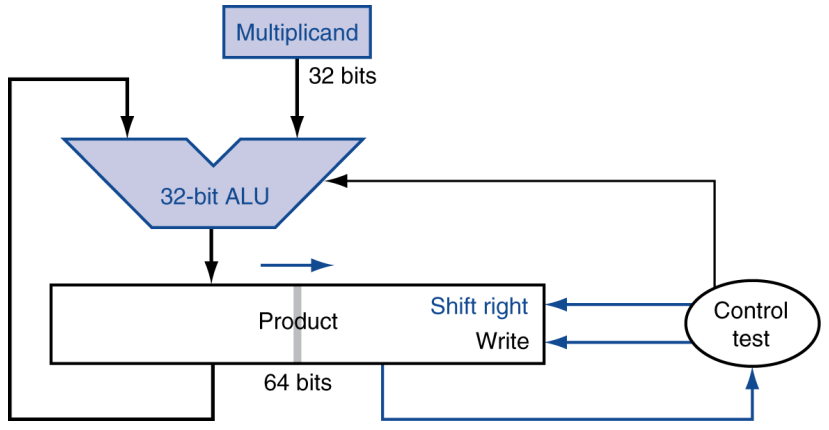
- 부분 product 추가당 1사이클
- 곱셈의 빈도가 낮으면 괜찮다.
- multiplicand와 ALU가 32비트로 줄었다.
최적화 multiplier 예제
- 4 X 3 = 0100_2 x 0011_2 = 0000 1100_2 (=12)
- multiplicand : 0100
- multiplier : 0011
- 처음에 multiplier인 0011이 세팅된다.
0 : 0000 0011
- LSB가 1이면 상위 4비트에 multiplicand를 더한다.
- 그리고 shift right 수행한다.
1 : 0100 0011 → 0010 0001
2 : 0110 0001 → 0011 0000
3 : 0011 0000 → 0001 1000
4 : 0001 1000 → 0000 1100
- 단점 : 32비트면 32번 반복해야한다. → 느리다.
빠른 multiplier
- 다중 가산기를 사용한다.
- 비용/성능 트레이드오프
- 각 자리별로 계산해서 더한다.
- 연산 횟수는 많지만 더 빨리 끝나고 비싸다.
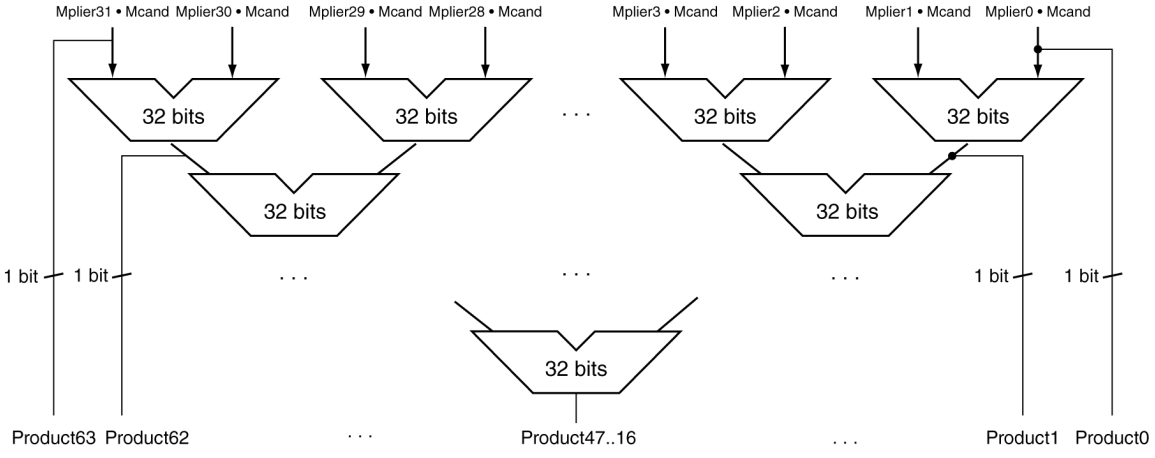
- 파이프라인을 사용한다.
- 여러 곱셈이 병렬로 수행된다.
MIPS 곱셈
- 곱셈에 대한 2개의 32비트 레지스터
- HI : 최상위 32비트
- LO : 최하위 32비트
mult rs, rt
multu rs, rt
- rs * rt의 결과가 HI / LO 레지스터에 저장된다.
- 32비트 * 32비트 = 64비트
mfhi rd
mflo rd
- 각각 HI, LO의 값을 rd로 이동
- HI 값을 테스트하여 product가 32비트 오버플로되는지 확인할 수 있다.
mul rd, rs, rt
- rs * rt 곱의 최하위 32비트 값을 rd로 이동
나눗셈
- divisor가 0인지 확인
- 긴 나눗셈 접근 방식
- divisor(나누는 수) ≤ dividend(나누어지는 수)
- 몫의 1비트, 빼기
- 그렇지 않은 경우
- 몫이 0비트, 다음 dividend 비트를 내림
- divisor(나누는 수) ≤ dividend(나누어지는 수)
- 나눗셈 복원
- 빼기를 수행하고 나머지가 < 0이 되면 divisor를 다시 추가한다.
- signed 나눗셈
- 절대값을 사용하여 나누기
- 필요에 따라 몫과 나머지의 부호를 조정한다.
1001010 / 1000 = 1001 나머지 : 10
1001
┌────
1000 │1001010
-1000
─────
10
101
1010
-1000
─────
10
- dividend : 1001010
- divisor : 1000
- quotient : 1001
- remainder : 10
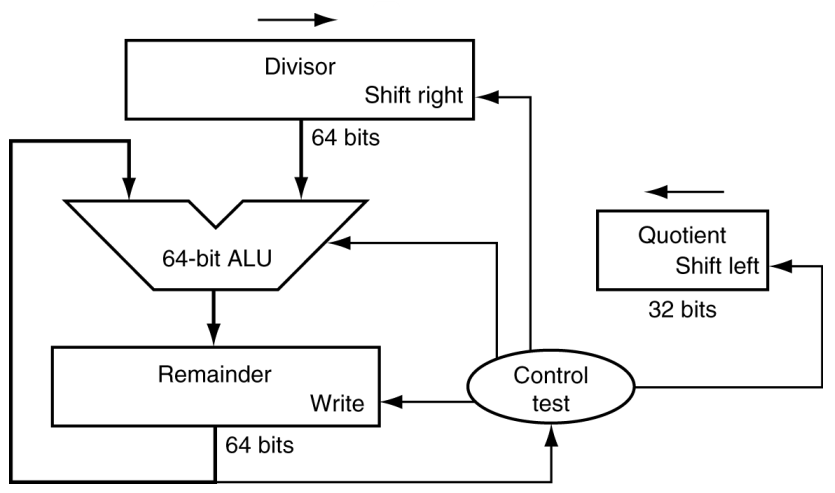
- 플로우 차트

최적화 Divider

- 나머지 뺄셈 per 1사이클
- multiplier와 매우 유사하다.
- 동일한 하드웨어를 두 가지 모두에 사용할 수 있다.
최적화 Divider 예제
- 예) 7 / 2 = 0111_2 / 0010_2 = Q : 0011_2, R : 0001_2
- dividend : 0111
- divisor : 0010
- quotient : 0011
- remainder : 0001
- 상위 4비트는 remainder
- 하위 4비트는 quotient
- 처음에 dividend인 0111이 세팅된다.
0 : 0000 0111
- shift left를 수행한다.
- 상위 4비트에서 divisor을 뺀다.
- 상위 4비트에 divior의 2의 보수 값을 더한다.
- 0010의 2의 보수 = 1101 + 1 = 1110
- MSB(sign 비트)가 1이면
- remainder가 음수이기 때문에 divisor을 빼주기 전의 초기값으로 복원해야한다.
- 상위 4비트 복원
- 상위 4비트에 divisor을 더한다.
- LSB는 0
- remainder가 음수이기 때문에 divisor을 빼주기 전의 초기값으로 복원해야한다.
- MSB(sign 비트)가 0이면
- LSB는 1
1 : 0000 1110 → 1110 111x → 0000 1110
2 : 0001 1100 → 1111 110x → 0001 1100
3 : 0011 1000 → 0001 100x → 0001 1001
4 : 0011 0010 → 0001 001x → 0001 0011
- remainder : 0001
- quotient : 0011
빠른 Divider
- 곱셈기처럼 병렬 하드웨어를 사용할 수 없다.
- 뺄셈은 나머지 부호에 따라 결정된다.
- 더 빠른 Divider(예: SRT 나눗셈)는 단계당 여러 몫 비트를 생성한다.
- 여전히 여러 단계가 필요하다.
MIPS 나눗셈
- HI/LO 레지스터를 사용
- HI : 32비트 나머지
- LO : 32비트 몫
div rs, rt
divu rs, rt
- 오버플로, 0으로 나누기 검사가 없다.
- 소프트웨어는 필요한 경우 검사를 수행해야 한다.
- mfhi, mflo를 사용
'컴퓨터시스템구조' 카테고리의 다른 글
| [컴퓨터시스템구조] 18. MIPS 부동 소수점 연산자 (1) | 2023.10.19 |
|---|---|
| [컴퓨터시스템구조] 17. 부동 소수점 (1) | 2023.10.15 |
| [컴퓨터시스템구조] 15. MIPS 배열 vs. 포인터 (0) | 2023.10.15 |
| [컴퓨터시스템구조] 14. MIPS Sort (1) | 2023.10.15 |
| [컴퓨터시스템구조] 13. MIPS 동기화 (0) | 2023.10.15 |
컴퓨터 산술
- 정수(integer) 연산
- 덧셈, 뺄셈
- 곱셈, 나눗셈
- 오버플로 처리
- 부동소수점 실수(Floating-point real number)
- 표현 및 연산자
산술 논리 장치(ALU)
- 정수 이진수의 산술/비트를 연산하는 조합 디지털 전자 회로
- CPU, FPU, GPU를 포함한 다양한 컴퓨팅 회로의 기본 구성 요소
- 하나의 CPU, FPU, GPU에는 여러 ALU가 포함될 수 있다.

정수 덧셈
- 예) 7 + 6
- 결과가 범위를 벗어나면 오버플로가 발생한다.
- '+', '-' 피연산자 더하기
- 오버플로 없음
- 두 개의 '+' 피연산자 더하기
- 결과 부호(sign bit)가 1인 경우 : 오버플로
- 두 개의 '-' 피연산자 더하기
- 결과 부호(sign bit)가 0인 경우 : 오버플로
정수 뺄셈
- 두 번째 피연산자 부정
- 예) 7 - 6 = 7 + (-6)
+7 : 0000 0000 ... 0000 0111
-6 : 1111 1111 ... 1111 1010
+1 : 0000 0000 ... 0000 0001
- 결과가 범위를 벗어나면 오버플로가 발생
- 2개의 '+' 또는 2개의 '-' 피연산자 빼기
- 오버플로 없음
- '-' 피연산자에서 '+' 빼기
- 결과 부호(sign bit)가 0인 경우 오버플로
- '+' 피연산자에서 '-' 빼기
- 결과 부호(sign bit)가 1인 경우 오버플로
오버플로 다루기
- 일부 언어(예: C)는 오버플로를 무시한다.
- MIPS에서 addu, addui, subu 명령어를 사용한다.
- 다른 언어(예: Ada, Fortran)에서는 예외 발생이 필요하다.
- MIPS에서 add, addi, sub 명령어를 사용
- 오버플로 시 예외 처리기를 호출한다.
- 예외 프로그램 카운터(EPC) 레지스터에 PC를 저장한다.
- 미리 정의된 핸들러 주소로 점프한다.
- mfc0(move from 코프로세서 레지스터) 명령은 EPC 값을 검색하여 수정 조치 후 반환할 수 있다.
멀티미디어를 위한 산술
- 그래픽 및 미디어 처리는 8비트 및 16비트 데이터 벡터에서 작동한다.
- 분할된 캐리 체인이 있는 64비트 가산기를 사용한다.
- 8x8비트, 4x16비트, 2x32비트 벡터에서 작동
- 하나의 64비트는 비싸기 때문이다.
- SIMD(단일 명령, 다중 데이터)
- 분할된 캐리 체인이 있는 64비트 가산기를 사용한다.
- 포화 연산(Saturating operations)
- 오버플로 시 결과는 표현할 수 있는 가장 큰 값이다.
- 참조) 2의 보수 모듈로 연산
- 예) FF FF FF(RGB) + FF FF FF(RGB) = FF FF FF(RGB)
- 흰색 + 흰색 = 흰색(표현할 수 있는 가장 큰값)
- 예: 오디오 클리핑, 비디오 채도
- 오버플로 시 결과는 표현할 수 있는 가장 큰 값이다.
- 크기가 매우 크다.
- 예) 비디오 색 계산
곱셈
- 긴 곱셈 접근법으로 시작
1000 x 1001 = 1001000
1000 # multiplicand
x 1001 # multiplier
────
1000
0000
0000
1000
────
1001000 # product
- multiplicand : 1000
- multiplier : 1001
- product : 1001000
- 곱의 길이는 피연산자 길이의 합
- 32비트 x 32비트 → 64비트

- 플로우차트

최적화 multiplier
- 병렬 단계 수행: add/shift

- 부분 product 추가당 1사이클
- 곱셈의 빈도가 낮으면 괜찮다.
- multiplicand와 ALU가 32비트로 줄었다.
최적화 multiplier 예제
- 4 X 3 = 0100_2 x 0011_2 = 0000 1100_2 (=12)
- multiplicand : 0100
- multiplier : 0011
- 처음에 multiplier인 0011이 세팅된다.
0 : 0000 0011
- LSB가 1이면 상위 4비트에 multiplicand를 더한다.
- 그리고 shift right 수행한다.
1 : 0100 0011 → 0010 0001
2 : 0110 0001 → 0011 0000
3 : 0011 0000 → 0001 1000
4 : 0001 1000 → 0000 1100
- 단점 : 32비트면 32번 반복해야한다. → 느리다.
빠른 multiplier
- 다중 가산기를 사용한다.
- 비용/성능 트레이드오프
- 각 자리별로 계산해서 더한다.
- 연산 횟수는 많지만 더 빨리 끝나고 비싸다.

- 파이프라인을 사용한다.
- 여러 곱셈이 병렬로 수행된다.
MIPS 곱셈
- 곱셈에 대한 2개의 32비트 레지스터
- HI : 최상위 32비트
- LO : 최하위 32비트
mult rs, rt
multu rs, rt
- rs * rt의 결과가 HI / LO 레지스터에 저장된다.
- 32비트 * 32비트 = 64비트
mfhi rd
mflo rd
- 각각 HI, LO의 값을 rd로 이동
- HI 값을 테스트하여 product가 32비트 오버플로되는지 확인할 수 있다.
mul rd, rs, rt
- rs * rt 곱의 최하위 32비트 값을 rd로 이동
나눗셈
- divisor가 0인지 확인
- 긴 나눗셈 접근 방식
- divisor(나누는 수) ≤ dividend(나누어지는 수)
- 몫의 1비트, 빼기
- 그렇지 않은 경우
- 몫이 0비트, 다음 dividend 비트를 내림
- divisor(나누는 수) ≤ dividend(나누어지는 수)
- 나눗셈 복원
- 빼기를 수행하고 나머지가 < 0이 되면 divisor를 다시 추가한다.
- signed 나눗셈
- 절대값을 사용하여 나누기
- 필요에 따라 몫과 나머지의 부호를 조정한다.
1001010 / 1000 = 1001 나머지 : 10
1001
┌────
1000 │1001010
-1000
─────
10
101
1010
-1000
─────
10
- dividend : 1001010
- divisor : 1000
- quotient : 1001
- remainder : 10

- 플로우 차트

최적화 Divider

- 나머지 뺄셈 per 1사이클
- multiplier와 매우 유사하다.
- 동일한 하드웨어를 두 가지 모두에 사용할 수 있다.
최적화 Divider 예제
- 예) 7 / 2 = 0111_2 / 0010_2 = Q : 0011_2, R : 0001_2
- dividend : 0111
- divisor : 0010
- quotient : 0011
- remainder : 0001
- 상위 4비트는 remainder
- 하위 4비트는 quotient
- 처음에 dividend인 0111이 세팅된다.
0 : 0000 0111
- shift left를 수행한다.
- 상위 4비트에서 divisor을 뺀다.
- 상위 4비트에 divior의 2의 보수 값을 더한다.
- 0010의 2의 보수 = 1101 + 1 = 1110
- MSB(sign 비트)가 1이면
- remainder가 음수이기 때문에 divisor을 빼주기 전의 초기값으로 복원해야한다.
- 상위 4비트 복원
- 상위 4비트에 divisor을 더한다.
- LSB는 0
- remainder가 음수이기 때문에 divisor을 빼주기 전의 초기값으로 복원해야한다.
- MSB(sign 비트)가 0이면
- LSB는 1
1 : 0000 1110 → 1110 111x → 0000 1110
2 : 0001 1100 → 1111 110x → 0001 1100
3 : 0011 1000 → 0001 100x → 0001 1001
4 : 0011 0010 → 0001 001x → 0001 0011
- remainder : 0001
- quotient : 0011
빠른 Divider
- 곱셈기처럼 병렬 하드웨어를 사용할 수 없다.
- 뺄셈은 나머지 부호에 따라 결정된다.
- 더 빠른 Divider(예: SRT 나눗셈)는 단계당 여러 몫 비트를 생성한다.
- 여전히 여러 단계가 필요하다.
MIPS 나눗셈
- HI/LO 레지스터를 사용
- HI : 32비트 나머지
- LO : 32비트 몫
div rs, rt
divu rs, rt
- 오버플로, 0으로 나누기 검사가 없다.
- 소프트웨어는 필요한 경우 검사를 수행해야 한다.
- mfhi, mflo를 사용
'컴퓨터시스템구조' 카테고리의 다른 글
| [컴퓨터시스템구조] 18. MIPS 부동 소수점 연산자 (1) | 2023.10.19 |
|---|---|
| [컴퓨터시스템구조] 17. 부동 소수점 (1) | 2023.10.15 |
| [컴퓨터시스템구조] 15. MIPS 배열 vs. 포인터 (0) | 2023.10.15 |
| [컴퓨터시스템구조] 14. MIPS Sort (1) | 2023.10.15 |
| [컴퓨터시스템구조] 13. MIPS 동기화 (0) | 2023.10.15 |
