표현식(Expression)
- 표현식은 계산식이 값을 생성하거나 정의되지 않음(undefined; 종료에 실패)을 생성하는 구문 엔터티이다.
- 모든 프로그래밍 언어의 기본 구성 요소 중 하나이다.
- 함수형 언어처럼 명령문이 없는 언어도 있지만 모든 언어에는 표현식이 존재한다.
어떻게 표현하는가
- 연산자(Operator) 및 피연산자(Operands)
- x + y
- b - 1
- f(3) >= 0
- 전위, 중위, 후위 표기법
- 연산자의 위치를 기준으로
- 전위 : <prefix> ::= <op><prefix><prefix> | ...
- 중위 : <infix> ::= <infix><op><infix> | ...
- 후위 : <postfix> ::= <postfix><postfix><op> | ...
표기법(Notation)
- 수학 방정식 : a + b * c + d
- 중위 표기법 : (a + b) * (c + d)
- 전위 표기법 : * + a b + c d
- 폴란드 표기법(Polish notation(PN))
- 케임브리지 폴란드 표기법 : 연산자를 괄호 안에 넣는다.
- (* (+ a b) (+ c d))
- 후위 표기법 : a b + c d + *
의미론(Semantics)
- 표현식의 의미(또는 계산 방법)는 표기법에 따라 변경될 수 있다.
- 예를 들어, 괄호가 없는 중위 표현식은 계산시 모호함을 유발할 수 있다.
- a + b * c + d
- 1번 해석 : a + (b * c) + d
- 2번 해석 : (a + b) * (b + c)
- 중위 표기법에서는 연산자의 우선순위(Precedence)와 연관성(Associativity)을 고려해야 한다.
우선 순위(Precedence)
- 연산자 우선 순위는 어떤 연산자를 먼저 고려해야 하는지 결정한다.
- 표현의 계산이 우리의 직관과 일치하도록 우선 순위를 정의한다.
- 1 + 2 * 3
- 1번 해석 : 1 + (2 * 3) = 7
- 2번 해석 : (1 + 2) * 3 = 9
- 우리는 값이 9가 아닌 7이 되기를 바란다.
- 따라서 이러한 경우를 방지하기 위해서는 우선순위 규칙이 필요하다.
연관성(Associativity)
- 그러나 표현식을 올바르게 계산하기에 우선순위는 충분하지 않다.
- 그래서 연산자가 피연산자와 어떻게 연관되는지 알려주는 연산자 연관성을 고려해야 한다.
- 10 - 5 - 3
- 1번 해석 : (10 - 5) - 3 = 2
- 2번 해석 : 10 - (5 - 3) = 8
- 대부분의 산술 연산자는 왼쪽에서 오른쪽으로 연관된다.
- 하지만 지수화와 같은 경우도 있다.
- 5^3^2
- 1번 해석 : 5^(3^2)
- 2번 해석 : (5^3)^2
우선순위와 연관성
- 대부분의 언어는 직관적인 우선순위와 연관성을 가지고 있다.
- 코드를 작성할 때 이를 신중하게 고려해야 한다.
- 의심스러운 점이 있으면 괄호를 사용하여 의도를 명확히 하는 것이 좋다.
- 괄호를 잘 사용하면 항상 코드 가독성이 높아집니다.
- (1 + 2) * 3
- (10 - 5) - 3
- (5^3)^2
전위 표기법(Prefix)
- 중위 표기법과 달리 전위 표기법은 연산자의 arity(피연산자 수)를 알고 있는 경우 모호성이 없다.
- 스택과 카운터를 사용하여 접두사 표현식을 계산하는 간단한 알고리즘을 고려할 수 있다.
- * + a 2 + b c
- a = 1, b = 2, c = 3
- Counter C = 0.
- 각 기호를 스택에 푸시한다.
- 연산자인 경우 C를 arity로 업데이트한다.
- 각 피연산자 기호는 C를 감소시킨다.
- C = 0이면 연산자를 적용하고 결과 R을 스택에 저장한 다음 사용된 기호를 삭제한다.
- 새로운 연산자를 위해 C 업데이트한다.

- *는 연산자이고 필요한 연산자 수는 2. (C=2)
- +는 연산자이고 필요한 연산자 수는 2. (C=2)
- a는 피연산자이므로 C 감소. (C=1)
- 2는 연산자이므로 C 감소. (C=0)
- C가 0이므로 연산자를 적용한 결과(a+2=1+2=3)를 스택에 저장 후 기호 삭제
- 결과 값 3은 피연산자이므로 이전 C(C=2)에서 감소. (C=1)
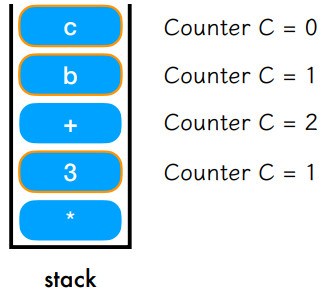
- +는 연산자이고 필요한 연산자 수는 2. (C=2)
- b는 피연산자이므로 C 감소. (C=1)
- c는 피연산자이므로 C 감소. (C=0)
- C가 0이므로 연산자를 적용한 결과(b+c=2+3=5)를 스택에 저장 후 기호 삭제
- 결과 값 5은 피연산자이므로 이전 C(C=1)에서 감소. (C=0)
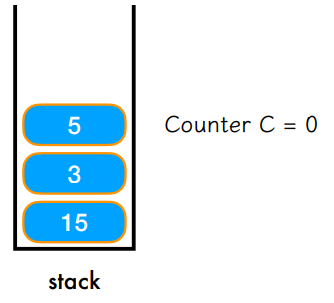
- C가 0이므로 연산자를 적용한 결과(3*5=15)를 스택에 저장 후 기호 삭제
후위 표기법(Postfix)
- 후위 표기법은 더욱 간단하다.
- 우리는 왼쪽에서 오른쪽으로 기호를 읽을 수 있고, 연산자를 만날 때마다 arity을 이전 피연산자에 적용한다.
- a b + c d + *, a = 1, b = 2, c = 3, d = 4
- a b + c d + *
- → 3 c d + *
- → 3 7 *
- → 21
구문 트리(Syntax Tree)
- 또한 표현식을 구문 트리로 구문 분석한 다음 이를 다른 표현식으로 고려할 수도 있다.
- 논리프 노드 : 연산자
- 리프 노드 : 피연산자
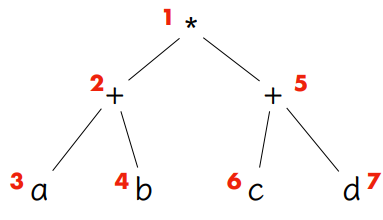
- 전위 표기법 : * + a b + c d

- 중위 표기법 : a + b * c + d
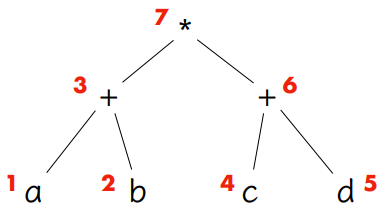
- 후위 표기법 : a b + c d + *
표현식 계산
- 수학에서 a - b + c와 a + c - b는 다른 결과를 갖지 않으며 수학적으로 동일하다.
- 그러나 프로그래밍 언어 표현식에서는 이러한 하위 표현식 계산 순서가 실제로 결과를 바꿀수 있다.
- 따라서 하위 표현식 계산 순서를 고려해야 한다.
- 우리가 조심해야 하는 데에는 몇 가지 이유가 있다.
1. 부작용(Side Effect)
- 명령형 언어에서는 계산 자체가 부작용을 통해 변수 값을 수정하는 것이 가능하다.
- (a + b++) * (c + b--)
- (a + f(b)) * (c + f(d))
- 프로그램의 구성 요소가 실행되어 프로그램의 상태를 수정하면 부작용이 발생한다.
2. 유한 산술(Finite Arithmetic)
- 컴퓨터에서 표현되는 숫자는 유한하다.
- 예) C에는 다양한 범위의 정수를 나타낼 수 있는 short, int, long과 같은 다양한 정수 유형이 있다.
- 계산 결과(또는 하위 표현식 계산)가 경계를 초과하는 경우 오버플로 또는 언더플로가 발생한다.
- a-b+c , a > b > c
- 1번 해석 : (a-b)+c
- 2번 해석 : (a+c)-b
- 컴퓨터에서 2번은 (a+c)가 범위를 벗어나면 문제가 있을 수 있다.
3. 정의되지 않은 피연산자(Undefined Operands)
- 연산자 적용의 두 가지 전략: 조급한 계산법(eager evaluation), 지연 계산법(Lazy Evaluation)
- 조급한 계산법(Eager Evaluation) : 먼저 모든 하위 표현식을 계산한 다음 연산자를 적용
- 지연 계산법(Lazy Evaluation) : 나중에 하위 표현식의 계산
- a == 0 ? b : b/a
- 조급한 계산법으로 모든 피연산자를 먼저 계산하면 b/a를 계산할 때 0으로 나누기가 정의되지 않으므로 오류가 발생한다.
- 그러나 지연 계산법으로 계산해야 하는 피연산자만 계산하면 괜찮다.
- a == 0이면 b
- a != 0이면 b/a
4. 단락(Short-circuiting)
- 단락(Short-circuiting)은 다른 표현식을 계산할 필요가 없을 때 부분 표현식만 계산하는 기술이다.
- if(str != null && str.length() > 0) ...
- str != null이 만족되지 않으면 str.length()를 계산할 필요가 없다.
- 실제로 str != null 이전에 str.length()를 계산하면 문제가 발생한다.
5. 코드 최적화(Code Optimization)
- 하위 표현식 계산 순서는 코드 최적화를 고려하여 계산 자체의 효율성에 영향을 미칠 수 있다.
- a = array[i];
- b = a*a + c/d;
- a의 값은 메모리에서 읽어와야 한다.
- 따라서 a의 값이 a*a에 대해 메모리에 로드되는 동안 c/d를 먼저 계산하는 것이 더 효율적일 수 있다.
'프로그래밍언어론' 카테고리의 다른 글
| [프로그래밍언어론] 21. 제어 흐름(Control Flow) (0) | 2023.10.11 |
|---|---|
| [프로그래밍언어론] 20. 명령문(Statements) (0) | 2023.10.11 |
| [프로그래밍언어론] 18. 파이썬으로 CRT 구현 (0) | 2023.10.11 |
| [프로그래밍언어론] 17. 범위 규칙 구현(Scope Rule Implementation) (0) | 2023.10.11 |
| [프로그래밍언어론] 16. 동적 관리(Dynamic Management) (0) | 2023.10.11 |
